Exercises

The sketches can be opened with the Geometry app, so that you can move the dots around and rearrange the problem's drawing.

Easy

1. 

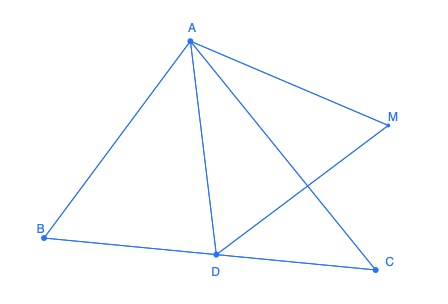
   In a triangle ABC, find the set of points M for which there exists a point D on line segment [BC] so that triangle BMD is equilateral.
   Sketch to download (that the app can open)

   Solution

   The rotations of line segment [BC] with center A and angle +60° and -60° describe the sets of such points M.

2. 

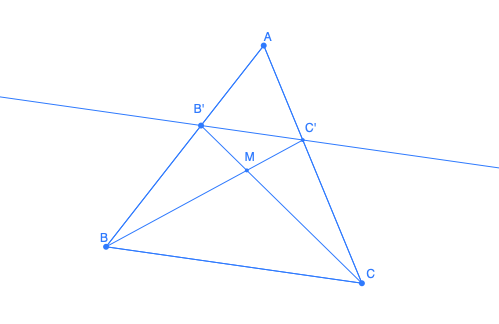
   In triangle ABC, the line D parallel to (BC) intersects [AB] in B' and [AC] in C'. The lines (BC') and (CB') intersect in M. Find the set of points M when D varies.
   Sketch to download (that the app can open)

3. 

   Let AB and AC be two arcs of a cercle. We assume that the length AB is strictly greater than BC. Let D be the middle of the arc AC and E be its orthogonal projection on [AB].
   Show that AE = EB + EC.
   Sketch to download (that the app can open)
   
   N.B: This theorem is due to Archimede.

Medium

1. 

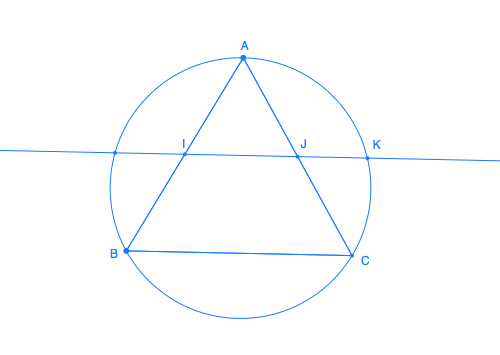
   In the equilateral triangle ABC, the line that passes by the middle I and J of [AB] and [AC] intersect in K the (small) arc (AC of the circle circumscribed to ABC. Show that IK/IJ = IJ/JK and find this value.
   Sketch to download (that the app can open)

Hard

1. 

   Let A be a point inside a circle C
   Let M be a point of circle C and D be the line segment bisector of [AM].
   Show that wherever M is, D is tangent to an ellipse. Give the focal and axis of the ellipse.
   Sketch to download (that the app can open)

2. 

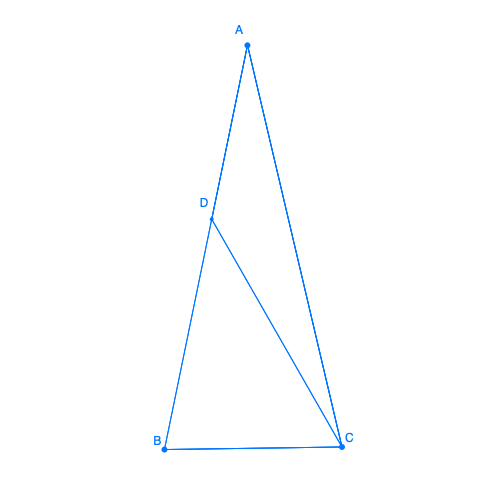
   Let ABC be an isocele triangle such that AB = AC and <CAB = 20°.
   Let D be the point on [AB] such that AD = BC. Determine angle <ACD.
   Sketch to download (that the app can open)